数学 I（三角法） を勉強していく上で思ったこととかメモ

三角関数の幾何的理解

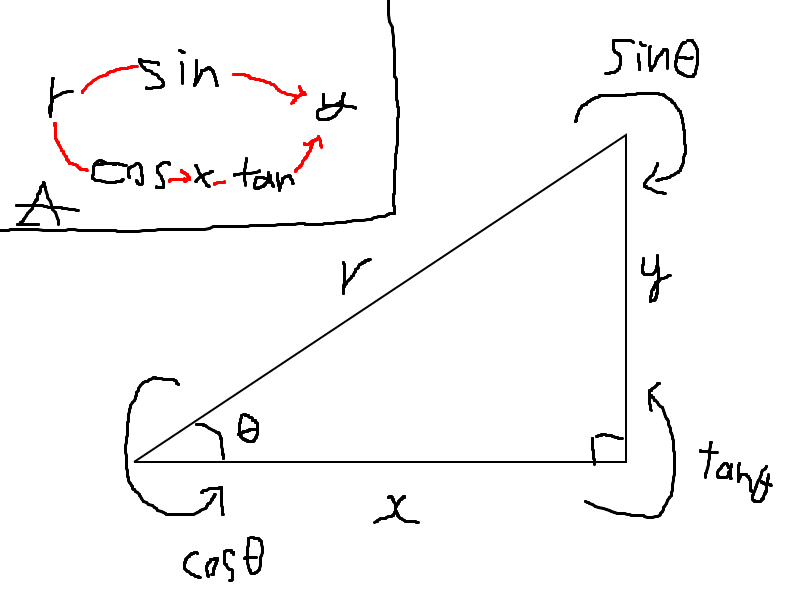
こんな感じに理解しました。

$$\text{sin}\theta: r \rightarrow y \\\text{cos}\theta: r \rightarrow x \\\text{tan}\theta: x \rightarrow y \\$$それぞれこんな感じに対象を飛ばす何かですね。逆に飛ばすものはその−１乗で考えることが出来ます4。もっと簡略化したのがAの図で、$$\tan \circ \cos = \sin$$が分かります。$90-\theta$の三角関数は上の図で$\theta$の場所を$\cos\theta$の場所から$\sin\theta$に移したものと考えられるため、法則も分ります。

凄い対称性を感じるので、群が見えるかな？とか色々な法則との同一性を調べてみたりしましたが特に何も見えませんでした。また後で色々考えたいみたいな気持ちになりました。

ベクトルで考えたりもした(余り意味はない、考えたので一応記録)$$\text{tat} = \cos\sin \\\text{sat} = \sin\tan \\\text{cat} = \cos\tan$$

ベクトルの合成は函数の合成を表しています。逆に飛ばす函数（逆関数ではない）は原点に対して反対のベクトルが考えられます。逆元もあって、単位元もありますが、図を見て分かるように色々掛け合わせていくと閉じてなくてどんどん右上（逆の函数は左下にも）伸びていきますので群はなしません。しかし対称性は確かにあるのでなんか引っかかります、、、因みに当たり前ですが上の図で正四角形を見た時にその頂点の函数は左下を起点として三角関数の関係があります。$$(\tan, \sin, \cos), (\tan^2, \text{sat}, \sin), (\text{sat}, \sin^2, \text{tat}), (\sin, \text{tat}, \cos^2), (\tan^2, \sin^2, \cos^2), ...$$のような感じでこれらはどれもある場所で三角関数とみなすことが出来ます。まぁ、$(\tan^2, \sin^2, \cos^2)$以外は各要素に何かの三角関数を掛けているだけなので自明ですが、、

二次三角関数と1についての法則

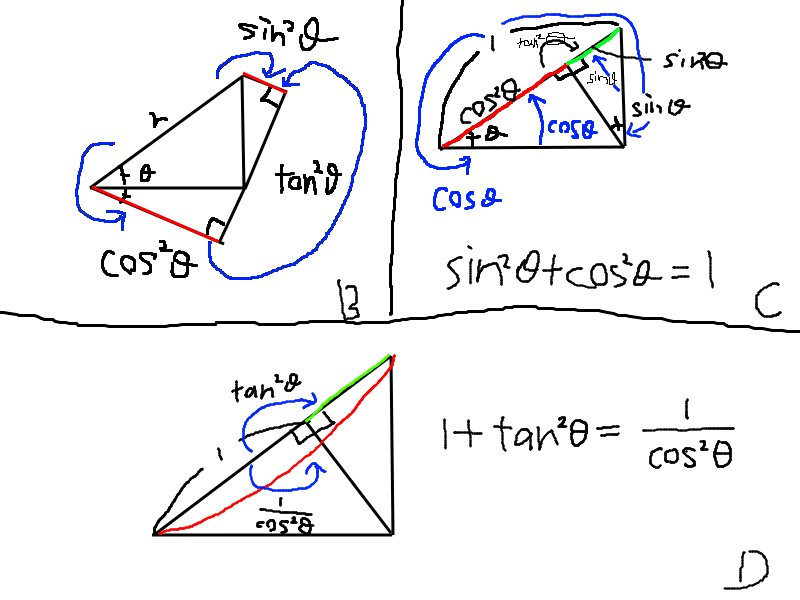
こんな感じに考えることが出来ます。Bは２次三角関数のイメージ、C,Dはそれぞれそれに係る法則たちを表しています。CはBを折りたたんだ形になっていることに注意して下さい。前章より、二次三角関数にも三角関数としての性質があるのでBを見るとわかりますが、$\sin^2 = \tan^2 \circ \cos^2$となっています。

この法則らは二次三角関数と1の関係について述べていますが、足し算が入ってるのでややこしいです。単純な函数の合成で考えられない。ここでも足し算とかけ算の関係について苦しめられるのか、、というお気持ちになった。

あと、角度の変更について貧弱な理解の仕方をしていると感じているので、そこら辺の理解は数IIの三角関数の方でやろうかと思っています。

高次三角関数

特に言うこともないですが、行き来するんですね行き来。因みに途中でひいてるどの線も垂線です。

$$\tan = \frac{\sin}{\cos} \\両辺をn乗して\tan^n = \frac{\sin^n}{\cos^n}$$tanはどの次数でもcosからsinに飛ばします。

180-theta, 90+theta

普通に反対の三角形とか横にした三角形を通じて理解しました。

正弦定理・余弦定理

どちらも、直角三角形についてしか考えられなかった三角関数を、どんな三角形でも考えたい！みたいなノリから生まれたのかなとか想像しました。

正弦定理

これは円を使えばどんな三角形も円の中に入れて回せば円周角の定理で直角三角形が作れることを利用してるのかな

B, Cについても同様にして$$\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R$$が分ります。

余弦定理

これが本当にわからなかったです。

10日間くらいいろいろ考えた（円を使う方法や変形する方法など）のですが、結局模範解答であろう垂線を引くやつで理解しました。1

三角形の面積

三角関数を使えば辺の長さが求められるので三角形の面積も、直角三角形でなくても求めることが出来る。$$S = \frac{1}{2}bc\sin A = \frac{1}{2}ac\sin B = \frac{1}{2}ab\sin C$$はまた垂線を引くことによって分かる。任意の三角形を直角三角形に変形する時に余弦定理の証明が出来なかった経験があるにも拘らず円を使おうとして時間を溶かしました。垂線を引くことで任意の三角形を上手く直角三角形に変形できます。

また、三角形の辺の長さa, b, cが分かっている時には$$s = a+b+cとすれば \\S = \frac{1}{2}bc\sin A,\ \sin^2A=1-\cos^2A,\ cosA =\frac{b^2+c^2-a^2}{2bc}から \\S = \frac{\sqrt{s(s-2a)(s-2b)(s-2c)}}{4}\qquad\qquad (1)$$が分かります。23

また、$2s = a + b + c$とすれば$$(1)でsを2sに取り替えて \\S = \sqrt{s(s-a)(s-b)(s-c)}$$でヘロンの公式を得ます。

三角形の面積とその内接円

特殊なケースなような感じもしますが、任意の三角形で内接円を考えると直角三角形がたくさんできるので計算して、rを内接円の半径として$$S = \frac{ar}{2} + \frac{br}{2} + \frac{cr}{2} = \frac{1}{2}r(a+b+c)$$が分かります。

まとめ

意外と楽しかったです。三角法は数A, IIでも出てくると思うので頑張りたいですね。

後印象的だったのは証明をしようとするのですが式がまとまらないという自体が発生するということです。今までこんなことは体験したことがなかったので、うーん、、となりました。当てはめれば解けるみたいなイメージがあったので。結局この式変形が苦手なままで証明すべき事をたくさん残したままでこれこそ無念って感じですが、、

次は統計ですね、これで数Iが終わる〜　ｶﾝﾊﾞﾘﾏｼｮｰ!

Notes

1 いつかはこの考え方でも証明したい、無念。 ↩

2 $(1-\cos A)(1 + \cos A) \\ = \frac{2bc-b^2-c^2+a^2}{2bc} \times \frac{2bc+b^2+c^2-a^2}{2bc} \\ = \frac{a^2-(b-c)^2}{2bc} \times \frac{(b+c)^2 - a^2}{2bc} \\ = \frac{(a-b+c)(a+b-c)(b+c-a)(b+c+a)}{4b^2c^2} \\ \sin A = \frac{\sqrt{s(s-2b)(s-2c)(s-2a)}}{2bc} \\ S = \frac{\sqrt{s(s-2a)(s-2b)(s-2c)}}{4}$ ↩

3 ここでの計算は$\cos^2 A$を計算すると因数分解で死ぬので$(1+cosA)(1-cosA)$を計算するのが良いなぁということなどを考えて、次数を減らすことの大切さを肝に銘じたりしました。 ↩

4 $\tan^{-1} \theta \neq (\tan \theta)^{-1}$本当にややこし ↩