積分で原始関数の差を求めると元の函数の面積が出る理由

微分とは

まずは微分です。微分はとても簡単ですし、微分だけでは何も広がらない気がします。

微分は函数の増加量を表す函数を得る作業のことです。函数$f(x)$に対して1、その各各点での増加量を表す函数は、$f'(x)$とか$\frac{df}{dx}$とか色々な記号で表して、$f(x)$の導関数と呼ばれます。

「増加量を表す函数」とはどういうことなのかと言うと、まぁこんな落書きをやったのですが：

これで、例えば左の函数を微分すると、右の函数が出るのです。注目してほしいのは右の座標軸で、これは左の座標軸と異なります。$\Delta y$すなわち$y$の増加量を縦軸にとって左の函数を表現したものが右の函数だと捉えることができます。まぁ３分間くらいは眺められますね。味もありますし。

では、これがちゃんと「増加量を表して」いるのか確認してみます。

例えば、赤の点$x=0$で、右の函数は$\Delta y = 0$です。左の函数を見てみると、$x=0$で変化がないことがわかります（頂点）。また、右の函数で$x=2$の時$\Delta y = 4$ですが、左の函数を見て$x=2$時点での函数の傾き（青の線の傾き）が4であることがわかります2。

全体的に函数を眺めて、導関数（右）は$x>0$で増加量が増加していますので、元の函数ではまるーく曲線を描くようになっているわけですね。

じゃあどうやってこの函数を求めるのかという話ですが、公式がわかっていますのでそれを参照しましょう。まぁ、いろいろな特別な函数の微分とかはありますが、多項式で書き表せる函数で基本となるのは$$f'(x) = knx^{n-1} \\where \ \ \ \ f(x) = kx^n$$

$$f'(x) = a'(x) + b'(x) \\where \ \ \ \ f(x) = a(x) + b(x)$$

らへんかなとおもいます。

式に従って、$$f'(x) = 6x + 5\quad where\quad f(x) = 3x^2 + 5x + 2 \\f'(x) = -x^{-2} = -\frac{1}{x^2} \quad where\quad f(x) = \frac{1}{x}=x^{-1} \\$$みたいな感じで簡単に多項式関数を微分することができます。

積分とは

次は積分です。積分は簡単に言うと微分の逆です。

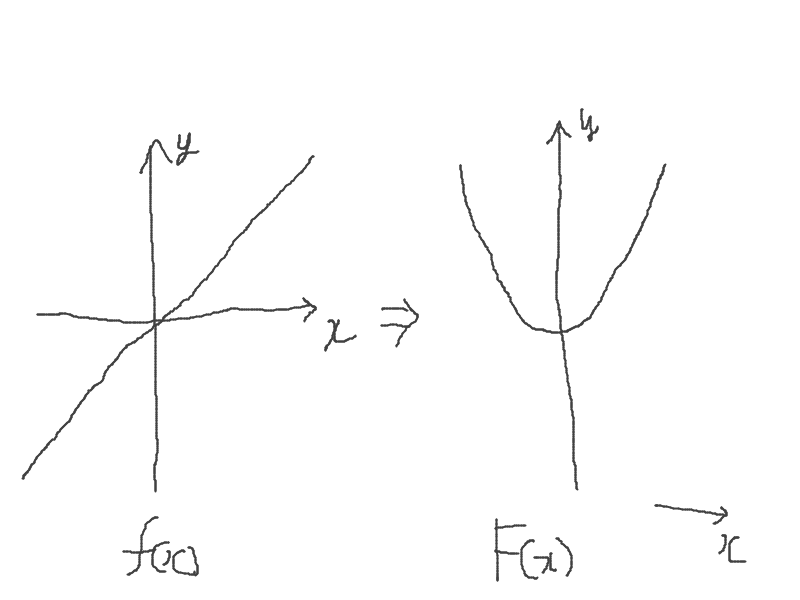
先程の図を逆にしたような感じの図です。なんにも考えずにただ逆を求めればよいのです。$f(x)$を積分して得られた函数を$F(x)$と書き表し、$f(x)$の*関数*います。

特に式を言う必要はなく、ただ逆をすればよいだけなのですが、定数は微分することで消えてしまうことに注意しないといけません。例えば左の函数が$f(x) = x$だったとすれば、$F(x) = \frac{1}{2}x^2 + C$となります。Cは定数であれば何でも良くて、これは微分によって消えてしまう情報なため、その逆をしようとすれば何になるかは分かりません。なので、一般的にこう書きます。落書きにx座標軸がないのもこのためです。元になる函数$f(x)$はあくまで$F(x)$の増減についてしか指定していませんので、絶対的な位置まではわからないのです。

任意の函数には、必ずそれに対する原始関数があるんだなぁ〜という意識も大切だと思います。全ての函数はそれぞれ他のある函数の増減を表しているとも考えられるのです。

ｱ、積分はこのように書き表されることもあります。$$F(x) = \int f(x) dx$$

ﾃｲｾｷﾌﾞﾝ!!! ﾃﾞｷﾙﾓﾝ!!!

この微積分たち、実は面白くて、まぁ知ってると思いますが、面積と大きな関係があります。

スバリ、任意の函数のグラフとx軸、$x=a$、$x=b$のグラフで囲まれる面積は、その原始関数の$x=a, b$それぞれの時点での値の差に等しいのです。

Figure 1.

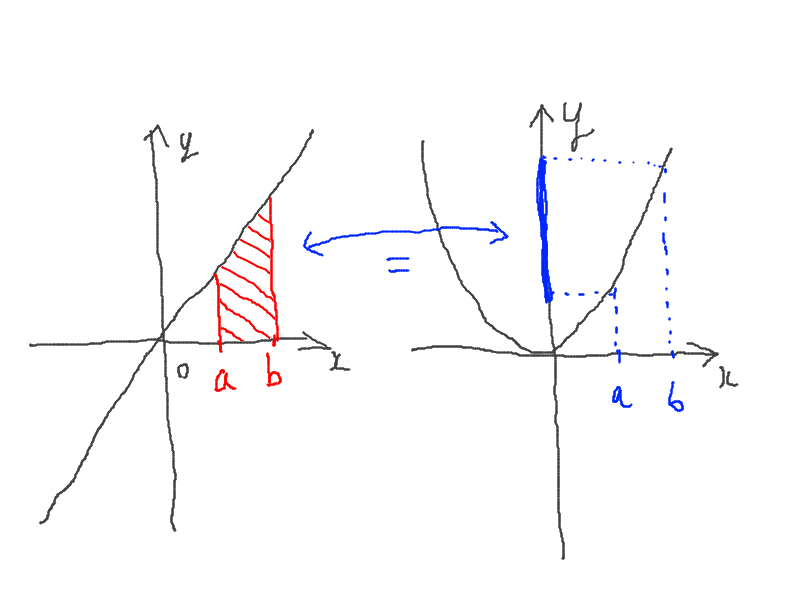
わかりにくいと思いますので、落書きで表すと以上のようになります。右の函数$f(x)$は左の函数の原始関数の１つです、簡単のため$C=0$であるような原始関数について考えていきますが、他の定数を持った原始関数も同じように議論することができます。

なんと、青で塗った線の長さと赤の面積の部分が等しいのです！とても面白い性質ですよね。

こんな性質を使って原始関数を使って面積を簡単に求めることを定積分といいます。こんな記号を使って表します。$$赤の部分 = \int_a^b f(x) dx$$また、上の図から分かる面白い性質もこの表記を用いて式として表しておきます。$$\int_a^b f(x) dx = F(b) - F(a) \qquad (1)$$

面白い性質はなぜ起こるのか

これを考えるには前段階として面積をきちんと定義しておく必要がありそうです。大体、上の図でも分かるとおり(1)の式は「長さ」と「面積」を比べてますので、:thinking:な顔になります。

面積は線に分解することが出来ると思います。しかし、幅０の線だといくら並べても面にならないので、幅が$k$で長さがあるような面に分解することが出来ると思いますと言い直します。なので、面積を「幅が$k$の面積の一つ一つの長さを足し合わせたもの」と最初はしようと思います。しかし、それだと、1x1の正方形を考えた時に、面積は$k$を1とすると1になり、$k$を0.5とすると2となってしまいます。面積値が分割する細かさに依存すると困るので、面積を「幅が$k$の面積の一つ一つの長さをそれぞれ$k$を掛けて足し合わせたもの」とします。すると、1x1の正方形で、$k=1$とすると1x1がひとつ出来るので面積は1、$k=0.5$としても、(0.5＊1) ＊ 2で1となります。

「長さ」と「面積」を比べる際は、単位を変えないで変換するのが自然でしょう。例えば、Figure 1で青く塗った線の長さが3cmのとき、面積は3cm^2としますよね。これは、線を*１の長方形*なしていることにも気が付きます。

では、きちんと定義できたので、この面白い性質について考えていきます。

まずは、函数と原始関数の関係（$\leftrightarrow$導関数と函数の関係）について考えてみます。

函数と導関数の関係

導関数は函数の各点の増加量を表す函数です。

そもそも、「増加量」ってなんでしょうか。

増加量は、中学で習いましたが、例えば$y$が$x$の函数のとき$y$の増加量は「$x$が１増加した時、$y$が増加する量」と定義されます。しかし、増加量は必ずしも１毎に変化していくわけではありません。事実、連続な函数として導関数が与えられています。なので、「x座標がxである点での増加量が$a$（$f'(x) = a$） （$\Leftrightarrow$ x座標がxである点の関数値はx座標がx+1である点の関数値より$a$小さい（$f(x+1) - f(x) = a$））」は、「とても小さい数$k$で$f(x)$の$x$から$x+k$までの増加量は$ak$」と言いかえると良い感じになります。

こう考えると、$f(x)$と$f'(x)$の関係性が見えてきて、$f(b)$は$a \le b$である適当な$b$を使えばその増加量から$f'(b)$を用いて$$f(b) = f(a) + \sum_{i \in \{ke\ |\ a \le ke \le b,\ e\in \mathbb{R}\}}kf'(i)$$と書けます。ここで、$k$を小さく取れば、面積の定義

幅が$k$の面積の一つ一つの長さをそれぞれ$k$を掛けて足し合わせたもの

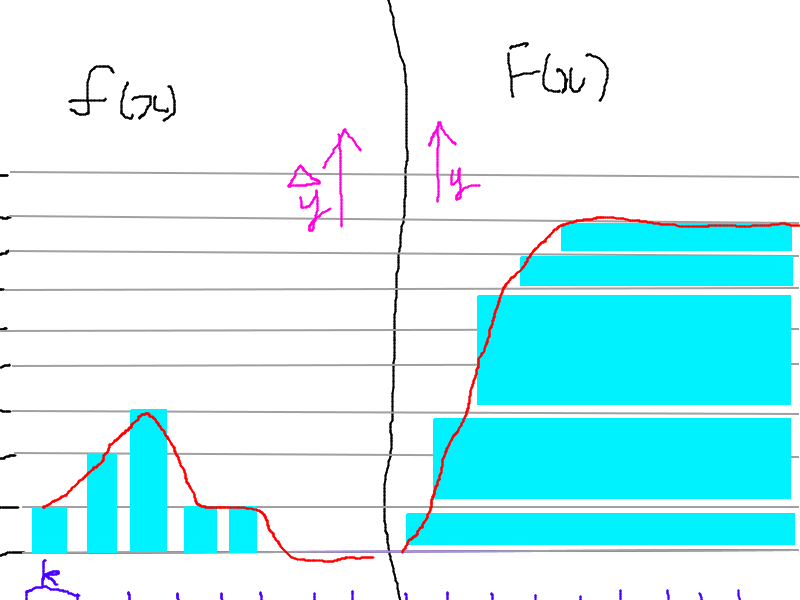
ちょっと分かり難いかもしれませんので、落書きをしき。右が左の函数の原始関数となっています。yの目盛りは灰色の線で横に書いています。また、xを区切っている目盛りが紫のやつで１つ分が$k$です。

原始関数のそれぞれのx位置での値は、そこまでの元の函数の値を全て足したものになっているのがわかります。例えば、左端で元の函数の値は1で原始関数の値は1、左から２番目で元の函数の値は２で原始関数の値は1+2=3となっています。その次は$f(x)$が３で$F(x)$が6=1+2+3となっていることから分かると思います。

気持ちはこんな感じで、あとはkをクッソ小さく取れば精度が上がりますねって話です。

まとめ

まぁ色々原理はありますが、とにかく定積分を使って嬉しいのは、面積という複雑な値を原始関数の値の差だけで求められるという点だと思います。また、微積分は本当に面白くてこれからも色々考えていこうと思っています。

微積分最初に発見した人興奮しただろーなーー

Notes

1 $f(x)$は函数ではなく、$f​$の関数値ですとかは言わないで >< ↩

2 誰がなんと言おうとわかりますので。 ↩