３次方程式の判別式

あなたの２次方程式の判別式はどこから？

２次方程式の場合、頂点の位置とか、解の公式とか、いろいろなところから導出することができました。

３次方程式にも同じ方法が使えないでしょうか。３次方程式の解の公式はできれば眺めたくないので、頂点の位置で考えてみたいと思います。（また、同じものを見ているので、こうして求まった３次方程式判別式は３次方程式の解の公式など他の導出方法からの理解ができます。ここらへん数学面白いですよね。また、どの方法が一番きつくないかがﾊﾟｯとわかる方法があれば良いなぁ）

実数解の個数

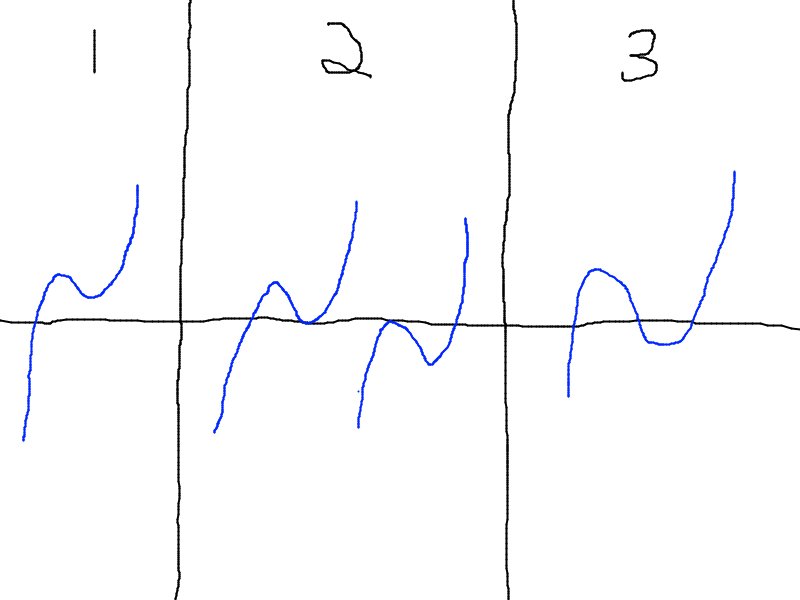
こんなグラフなので、実数解の個数が0ということはないですね。図のような場合が考えられると思います。何はともあれ、まずは極値点の位置を求めましょう。

極値点の位置

$$f(x) = ax^3 + bx^2 + cx + d$$

としておいて、微分して極値点を求めます。$$f'(x) = 3ax^2 + 2bx + c = 0　を解いて \\x = \frac {-b \pm \sqrt{b^2 -3ac}} {3a} \\２つの極値点は\ \Big(\frac {-b \pm \sqrt{b^2 -3ac}} {3a}, \frac{\pm(6ac-2b^2)\sqrt{b^2-3ac}+2b^3-9abc}{27a^2}+d \Big).$$$\pm\sqrt{b^2-3ac}$がたくさん出てくるのでこれを$\mathcal{X}$とおくと、極値点は$$\Big(\frac {\mathcal{X}-b} {3a}, \frac{-\mathcal{X}(2b^2-6ac)+b(2b^2-9ac)}{27a^2}+d \Big)$$と表せました（Desmosで一応チェック）。

あとは、このy座標を見れば良いでしょう。

解が１つになる時は、２つの極値を掛け合わせると正となることと同値です。

解が１つになる時は、２つの極値を掛け合わせると０となることと同値です。

解が１つになる時は、２つの極値を掛け合わせると負となることと同値です。

そして、２つの極値を掛け合わせたものが$$\frac{ - 18abcd + 4ac^3 + 4b^3d - b^2c^2}{27a^2}+d^2$$となり、つまりこれが３次方程式判別式となります。

まだ簡単にできるでしょうか。符号のみが大切なので、実数係数を仮定して$$-18abcd + 4ac^3 + 4b^3d - b^2c^2 + 27a^2d^2$$ともできると思います。

ここで、２次方程式判別式と見比べてみましょう$$b^2-4ac$$

何もわかりません。