線の長さを積分で考えてみる

線とは？　面積とは？

前回は、面積をとても細い長方形（線）の集合として見た時に、原始関数の値は元の函数においてその左側の値を細かく足していったものになっていることを確認しました。これのおかげで、複雑な面積という量を単純なある関数値の引き算として表すことが出来ていました。

同じようなものとして、線でも同じこと出来るんじゃね？ってことで、今回は線について考えていきます。

なぜ、急に線を持ち出してくるのかと言うと、線と面積がとても性質が似ているなと感じたからです。面積が細かい長方形（線）の集合ならば、線は細かい線（点）の集合だと考えることが出来るでしょう。なんか無限に足すーとかそういうのは原始関数が得意であることが前回わかったので、その続きとして自然だと思っています。

今回考えていく線

前回、面積を求めたときにも、何でも好きな面積を求められるというものではありませんでした。x軸と函数とx=aとx=bで囲まれている面積だけを求めることが出来ました。

今回の線もどんな線の長さでも求めることは出来ないと予測します。函数に起因しなければならないなら、普通に函数のある場所と場所のグラフ上での長さを考えてみます。

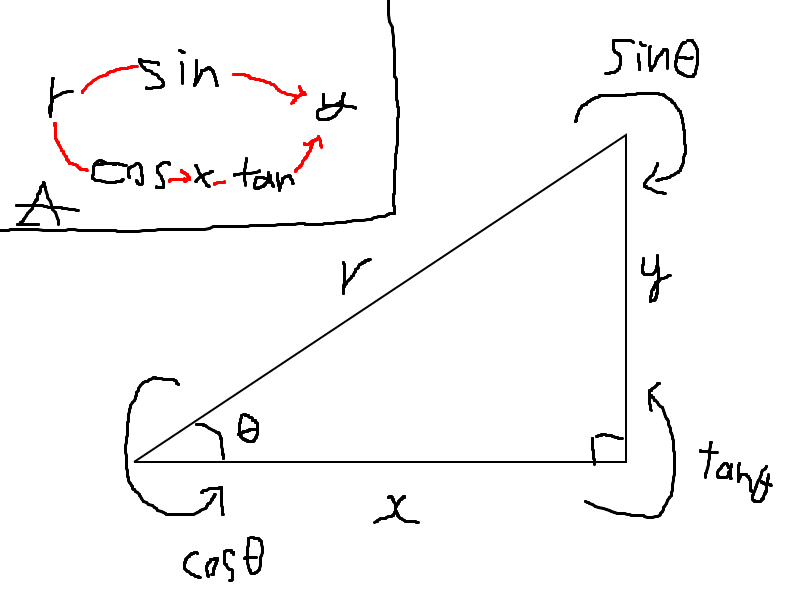
以下のような線を考えていきましょう。$f(x) = x^3 - 3x$です :

こんなグラフの赤線で塗った線の長さ$-1 \le x \le 2$の部分について考えます。

線の一個分

１つの線について考えてみる。

赤線のある箇所を拡大しまくると直線に見える。

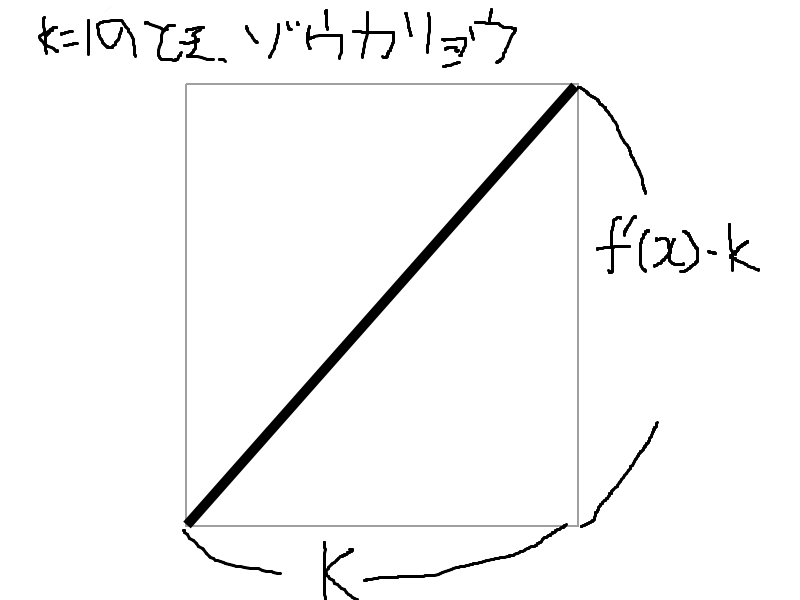
$f'(x)$はそれぞれの箇所の増加量を表しているので、また同じように精度$k$を使って、次のように考えることが出来る。$$xからx+kまでの線の長さ = \sqrt{(kf'(x))^2 + k^2}$$

全て足すのだが、積分をば

これを全てに対してやるので、前のやつと同じように考えて$$線の長さ= \sum_{i \in {ke\ |\ a \le ke \le b,\ e\in \mathbb{R}}} \sqrt{(kf'(x))^2 + k^2} \\= k \sum_{i \in {ke\ |\ a \le ke \le b,\ e\in \mathbb{R}}} \sqrt{f'(x)^2 + 1}\qquad(1)$$

と表すことが出来る1。ここで、前回の最終式を引っ張ってくる$$g(b) = g(a) + k\sum_{i \in \{ke\ |\ a \le ke \le b,\ e\in \mathbb{R}\}}g'(i) \\= g(a) + \int_a^b g'(x)\ dx \qquad (2)$$$f(b)$が$f(a)$から$f'(i)$を細かく足していって求められることを表している。

見て欲しいのは(1)と(2)が似ていることで、(1)は(2)で$g(a)=0$で$g(b)=線の長さ$、$g'(x) = \sqrt{f'(x)^2 + 1}$だと考えた場合の式と等しい。よって、(2)の２式目の変形が(1)に対して可能となる。

よって$$線の長さ = 0 + \int_a^b \sqrt{f'(x)^2 + 1}\ dx \\$$を得て、積分で単純に関数値の差として表すことが出来ることがわかった。

実際に計算してみる

今回の場合$f(x) = x^3 + 3x$で$a=-1,b=2$なのでこれで実際に計算してみる。$$f'(x) = 3x^2 + 3 \\\int_{-1}^2 \sqrt{(3x^2 + 3)^2 + 1}\ dx = \bigg[\frac{1}{2}x\sqrt{3x^2 + 4}+\frac{2\text{sinh}^{-1}(\frac{\sqrt{3}x}{2})}{\sqrt{3}} \bigg]_{-1}^2 = 18.3104$$このように簡単に導出することが出来ます（）2

まとめ

おそらく上の式では面倒なので、もう少し簡単な求め方を探してみたいと思います（正直こんな難しい式になると思ってなかった、、、）。

てか一通り書いて後から調べて知ったんですが、こういう函数の線の長さってｺﾁｮｳっていうんですねー。今回やったのは特別な場合だったみたいで、式が合ってて安心した。ﾊﾞｲｶｲﾍﾝｽｳﾋｮｳｼﾞとか言うわけわからないものも書いていました、、、

面積ととても似ていたので同じような感じでいけるかなぁと思ってたら大間違いでしたね、、、

あとそろそろ極限についてちゃんとやらないと死んでしまいそうなので極限もやります。

Notes

1 二番目の式変形は$0 \le k$であることを利用しています ↩

2 勿論これはWolframさんの答えです。根号を含んだ函数の積分なんて僕知らない >< ↩